This article is the second in a two-part series on two testing standards that can improve the data gathering and evaluation process for tire performance testing in winter conditions. Part One discussed ASTM F1572, a standardized test method for evaluating the performance of tires on snow and ice, including straight-line acceleration and braking, step steer, slalom, hill climb and road circuit handling. Part one can be read here.
On-vehicle performance testing for tires presents unique challenges when it comes to consistency. Much of this testing occurs outside of a controlled laboratory environment. Test programs can extend over days or weeks, during which time environmental and test conditions can vary significantly. For tire performance comparisons to be successful, it is paramount to investigate and adjust for systemic or bias variations. This is especially important when testing tires in winter conditions such as snow and ice. Ambient air temperature, snow temperature, solar load, snow compaction and other factors can change dramatically from hour to hour.
ASTM F1650 offers an in-depth procedure to determine and correct for significant variations in a testing environment by developing correction factors based on control tire data. This method can improve the data evaluation process for tire performance testing in winter conditions and give a means to post-process the data. ASTM F1650 has two methods for determining and correcting for variations, A and B, both of which have similar function and calculations. These methods produce different absolute traction values but provide the same relative traction ratings from a rank-order perspective. Both methods can use either two or three test samples (Tn) between control test runs (Cn).
FIGURE ONE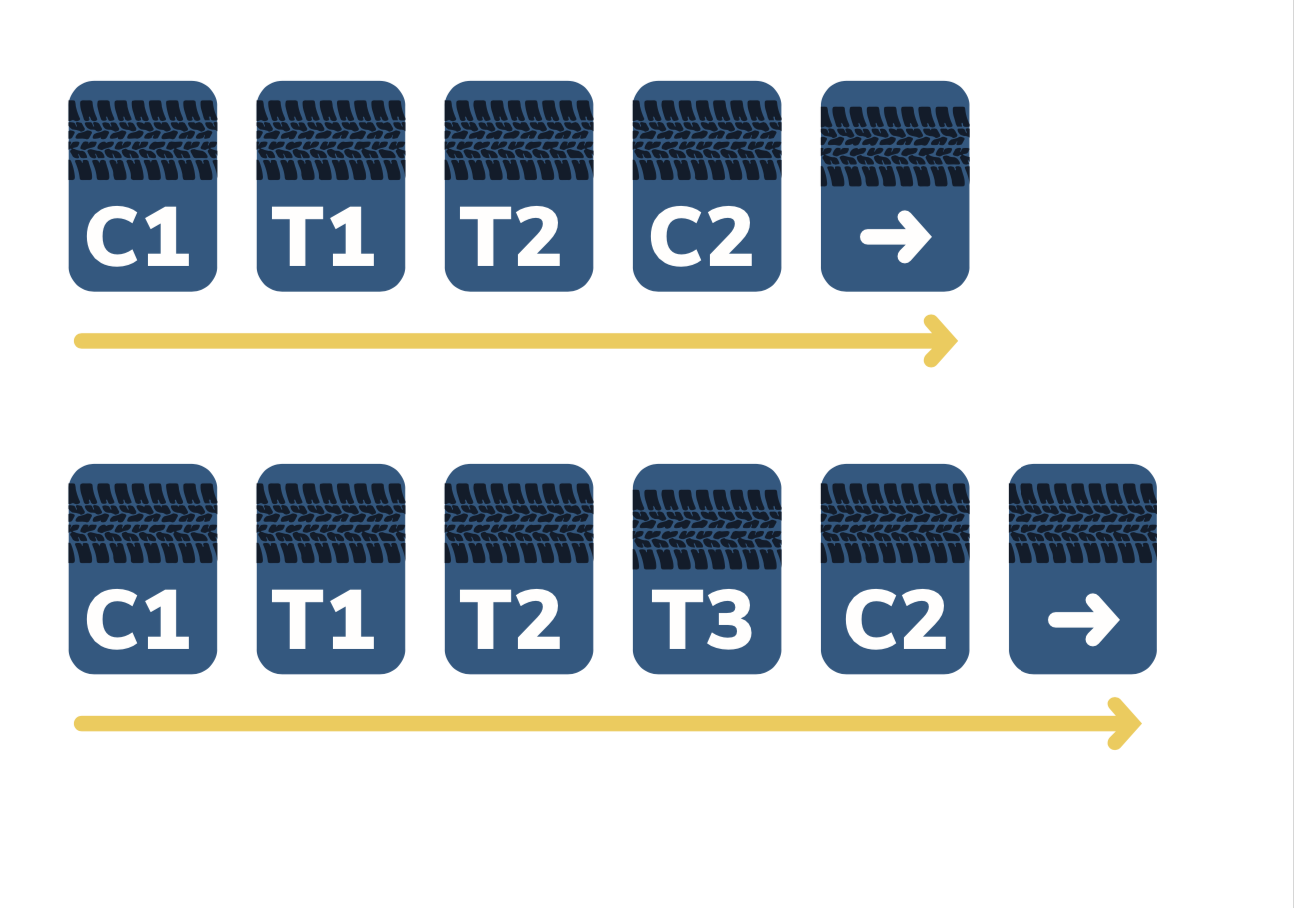
Method A and Method B can both be used for linear or transient error on control tires. The main difference is the control tire reference choice: Method A (figure 2) uses the first control tire run as a reference, whereas Method B (figure 3) uses an average of all control tire runs as a reference. Another difference is that Method B requires no test for statistical significance and makes corrections to all runs. Method A only makes corrections if there is significant error or drift.
Method A
Method A uses data from the first control tire as a reference point. A good evaluation will include at least five control set values (C1, C2 … C5). Plotting the control points helps to create a sense of any patterns. Figure 2 shows an example of control data with no significant trend, good precision and a coefficient of variation of less than 1%.
FIGURE TWO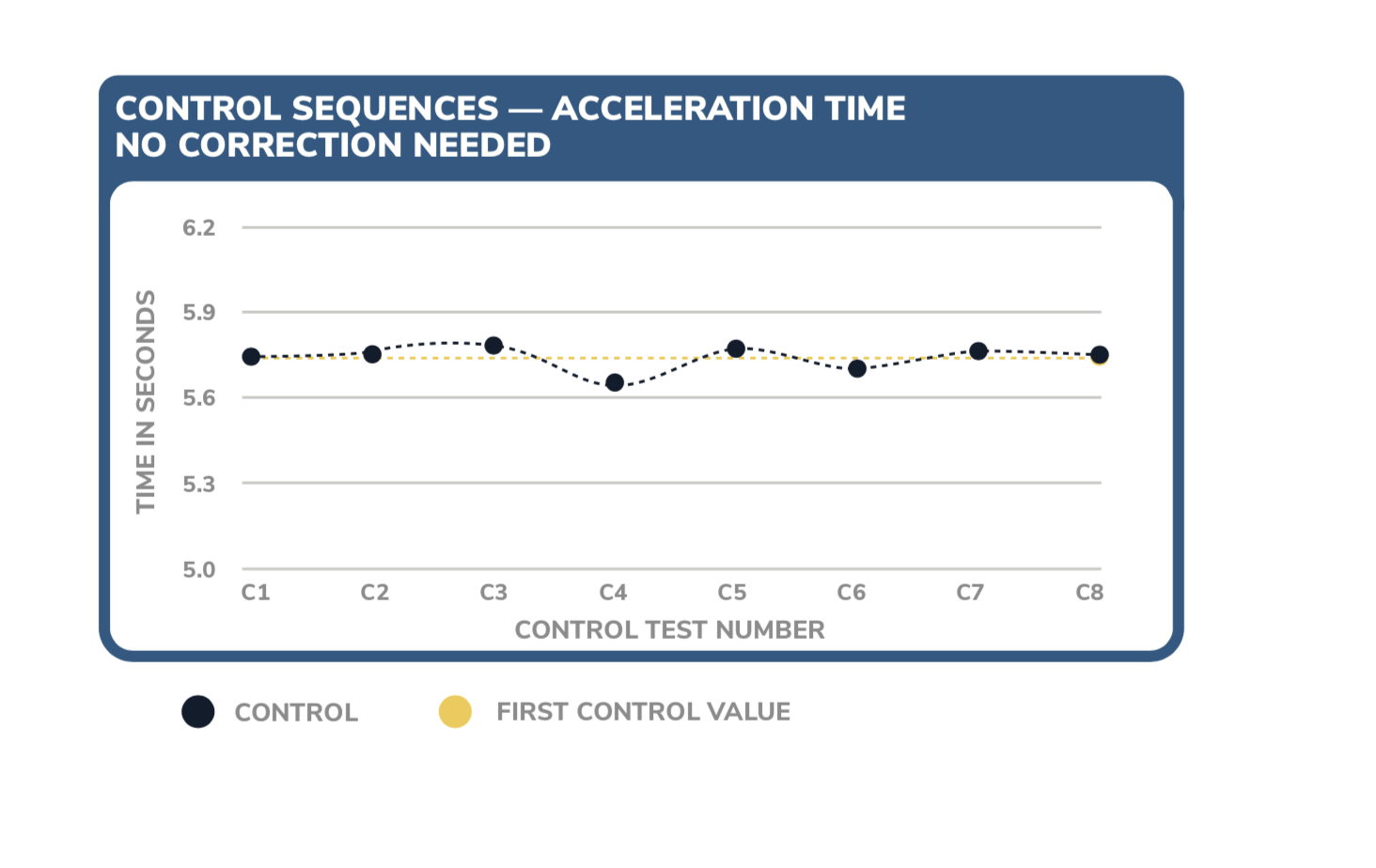
FIGURE THREE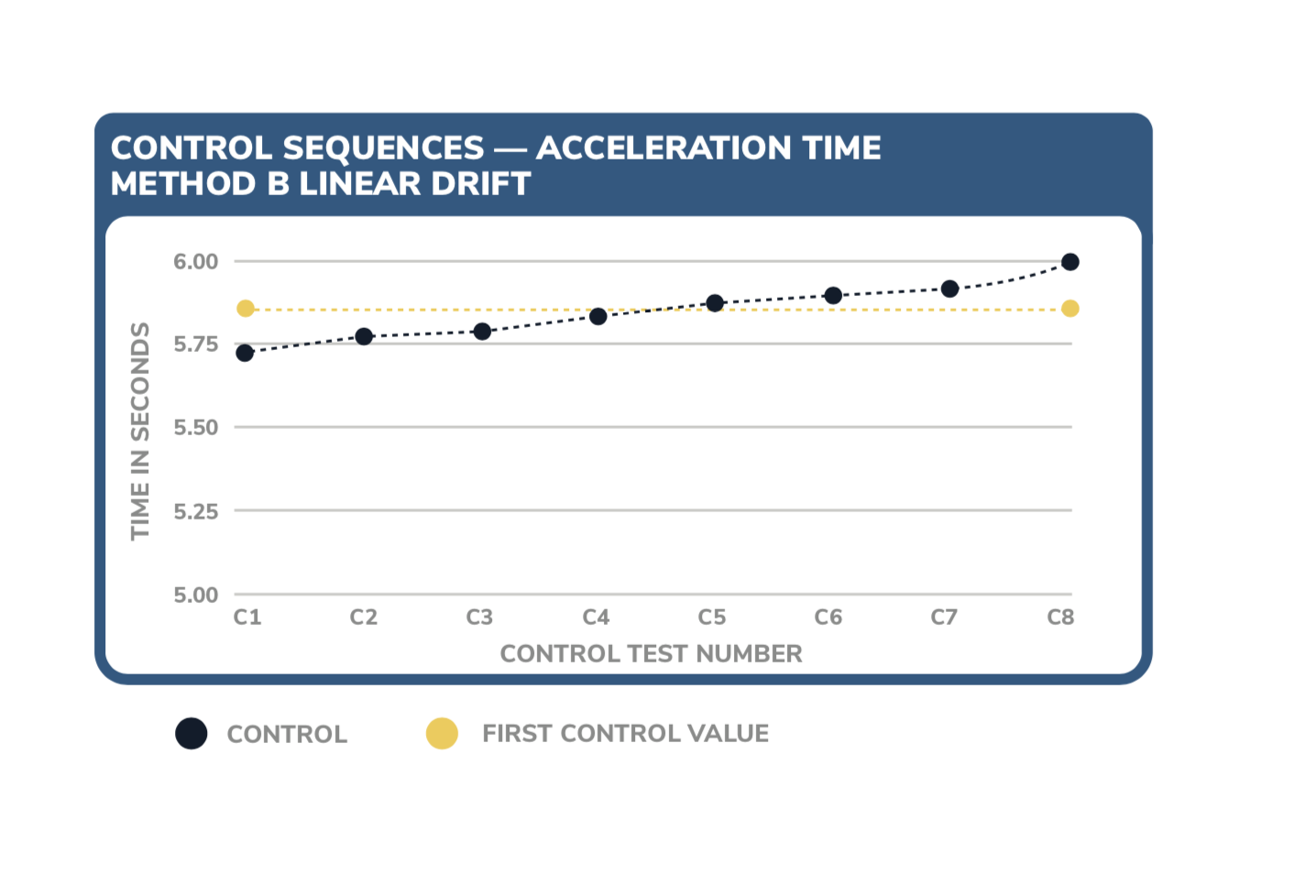
The example in Figure 2 would not need correction. However, not all data sets maintain this level of fidelity. There are several types of drift or shift that can occur in control data sets: linear, type 1 and type 2. ASTM F1650 has different mechanisms to check for and adjust significant drift depending on which type of drift has occurred, so it is crucial to accurately qualify drift.
Figure 4 shows a good representation of linear drift, meaning control values gradually increase with a slope over time.
FIGURE FOUR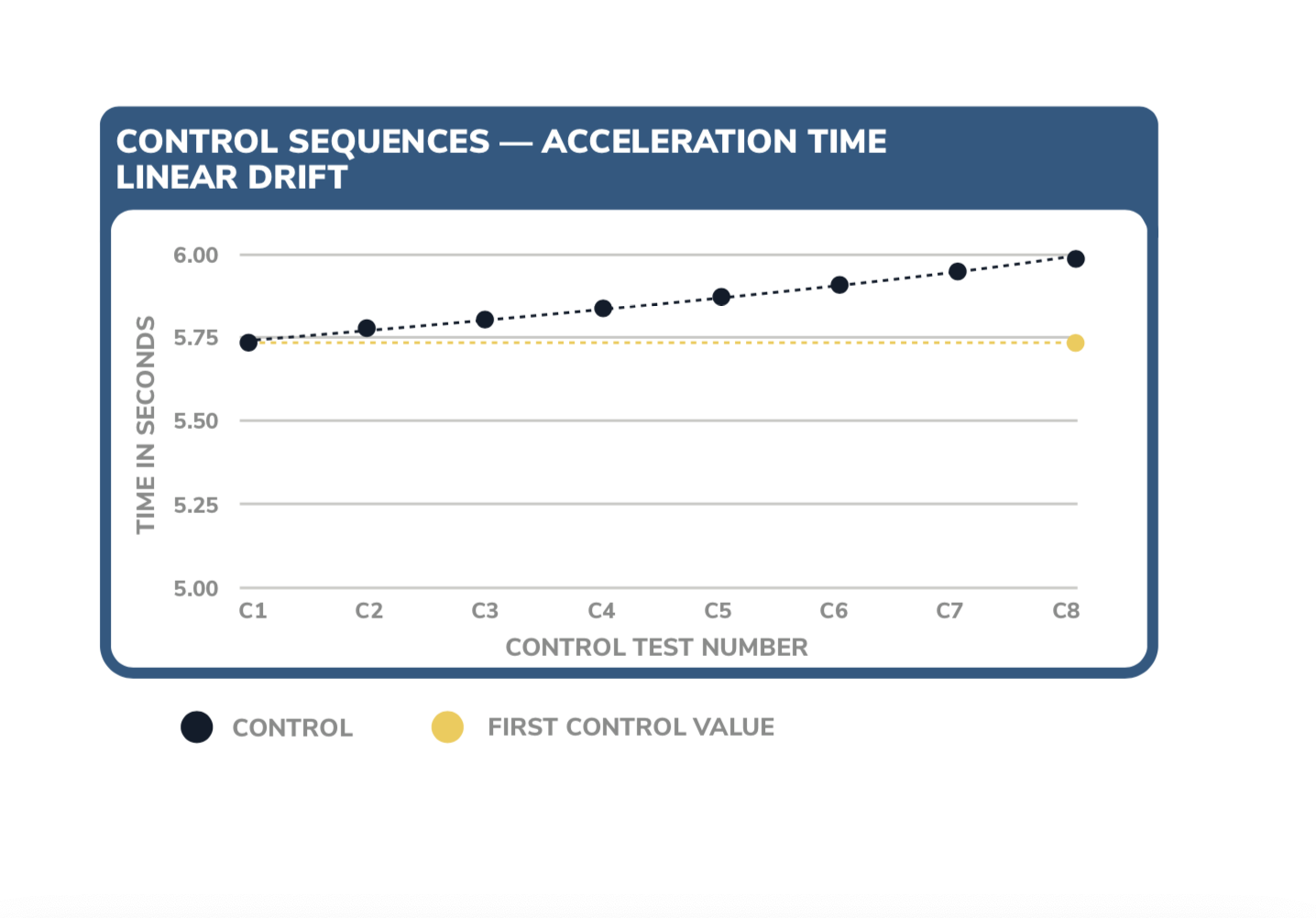
To evaluate the significance of linear drift, start by calculating the correlation coefficient (Rcalc). Determine the degrees of freedom and use that to find the tabulated Rcrit using a chart provided by ASTM F1650. If the Rcalc is greater than the Rcrit, then significant drift is considered present and corrections must be applied to test tire data.
Figure 5 shows a type 1 transient shift, which occurs when there is an abrupt shift in the data that returns to the prior trend. In this example, the transient shift occurs during the C4 and C5 control runs.
FIGURE FIVE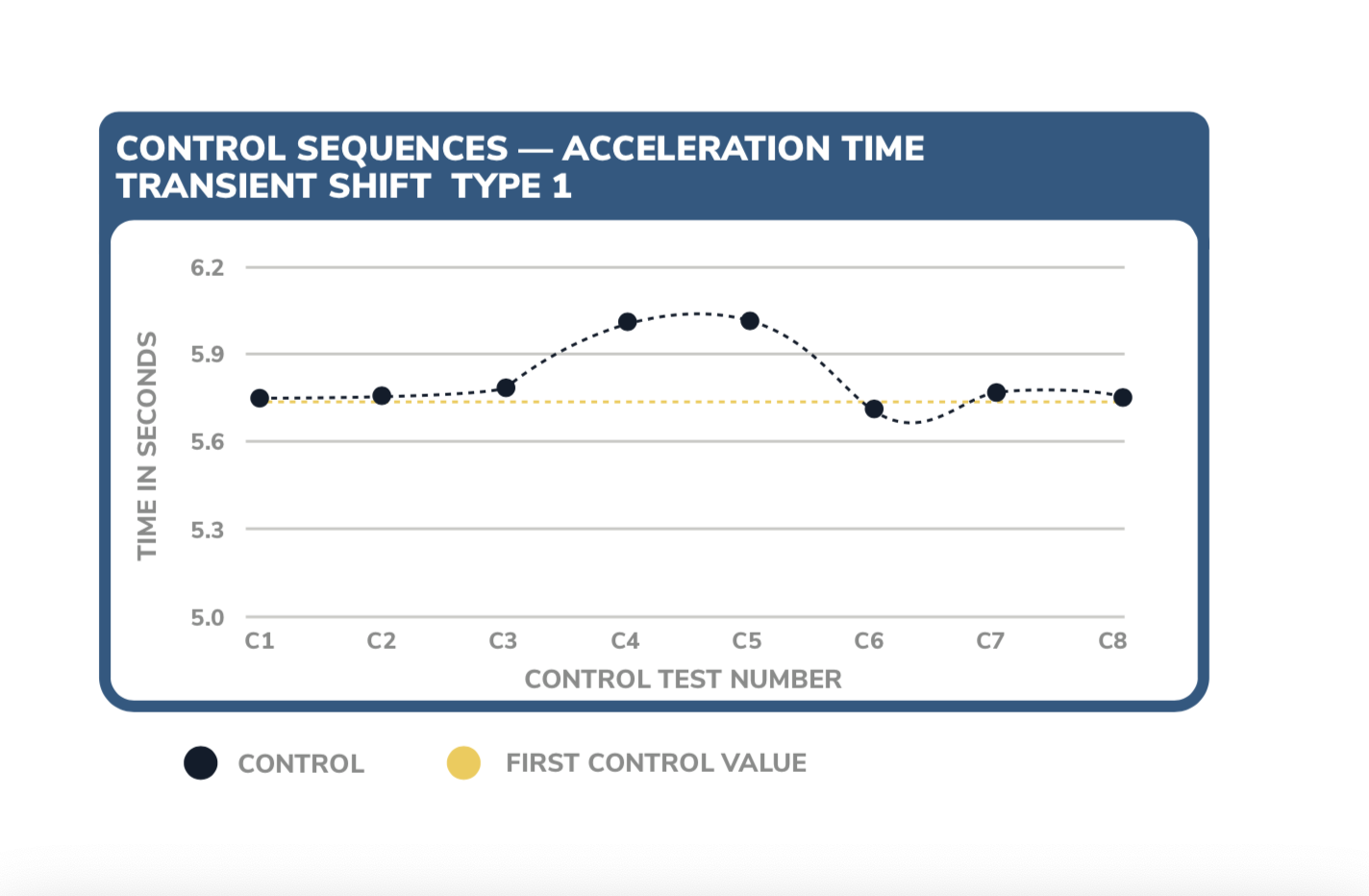
To evaluate type 1 shifts, calculate the standard error for the main regression line excluding the offset points. Calculate the standard error for the offset points if there are four or more. If less than three offset points, then take an average. There are two methods to determine transient shift significance depending upon the number of offset points. Both methods are covered in more detail in ASTM F1650 in section 8.4.4.1.
Figure 6 shows a type 2 transient shift, which occurs when there is a shift in data that does not correct to the previous trend. In this example, the drift begins during the C5 control run.
FIGURE SIX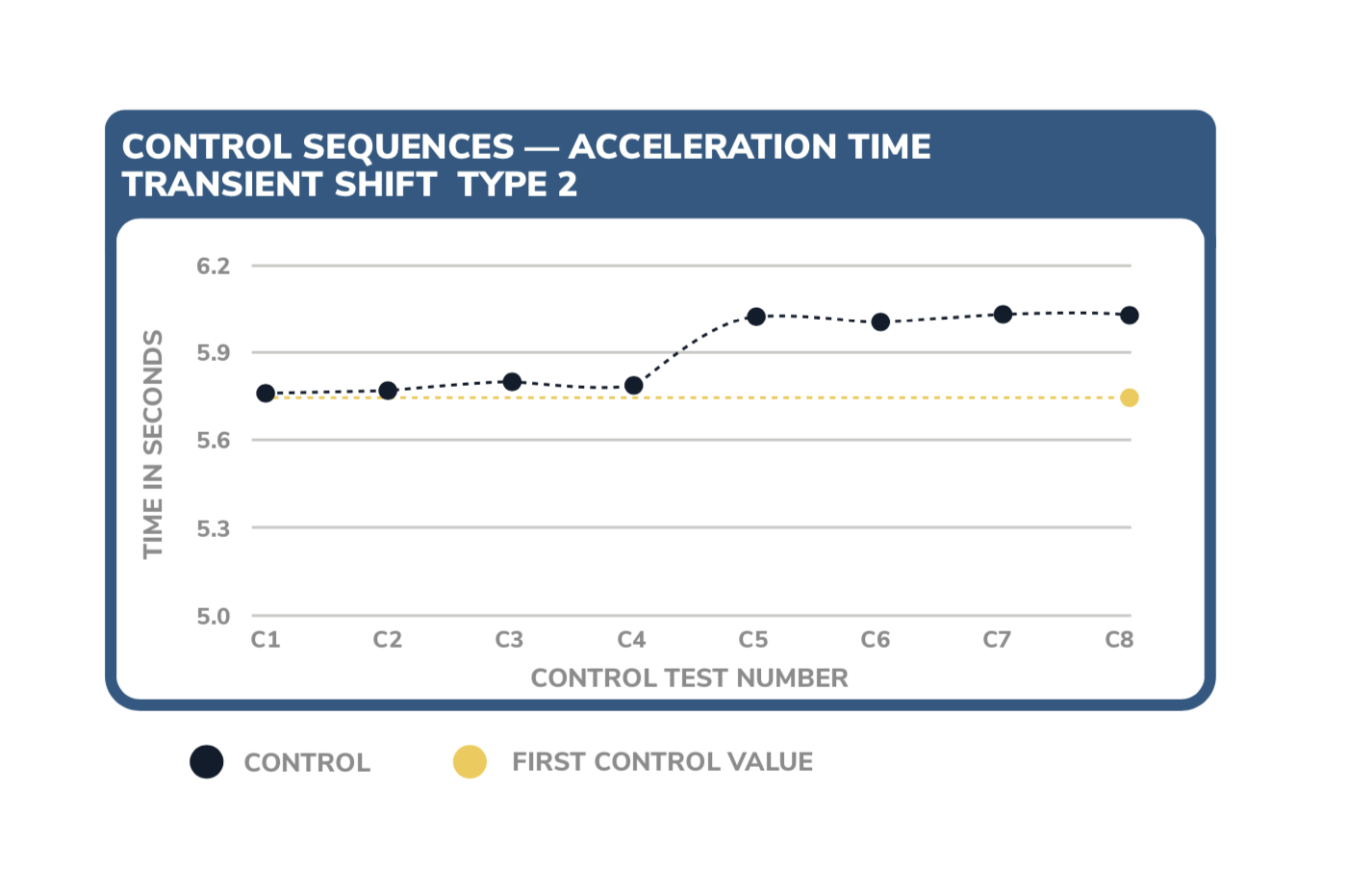
To evaluate a type 2 shift, calculate the standard error for each of the two trendlines. ASTM 1650 section 8.4.4.2 shows what conditions dictate whether drift is significant between the two trendlines at their point of offset.
For a drift or shift that is considered significant, ASTM F1650 section 8.5 has correction factors and an explanation on how to apply them. As seen in Figure 7, each pair of control runs (C1 and C2, C2 and C3, etc.) are summed and divided by two times the initial control reference, C1.
FIGURE SEVEN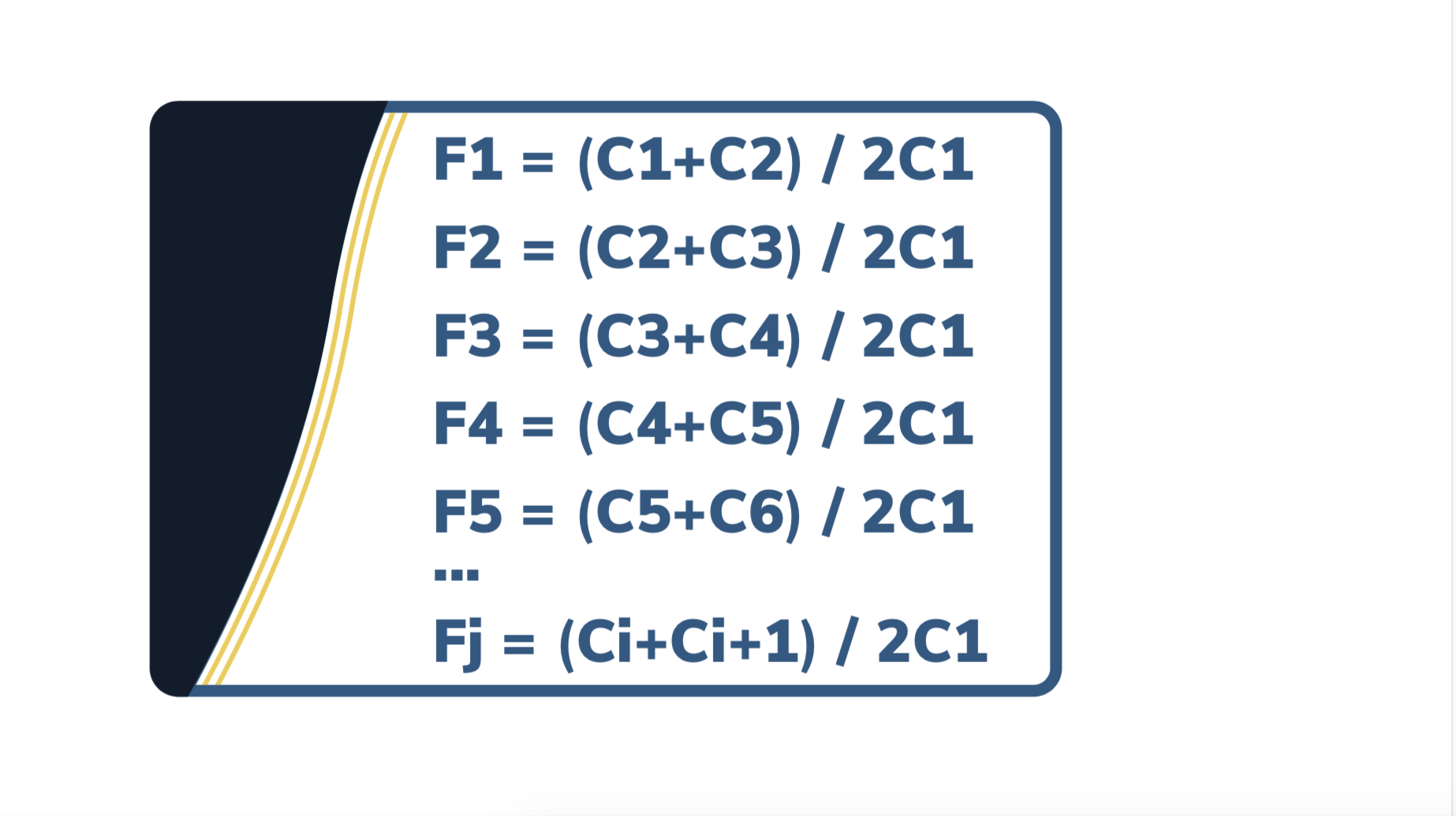
Method B
While Method A (Figure 2) uses data from the first control tire as a reference point, Method B (Figure 3) uses an average of all control test runs as the reference point.
Method B gives the same relative traction ratings as Method A, though the absolute traction ratings can be different. There are several benefits to choosing Method B. First, using an average as opposed to a single data point is more precise. Second, corrections are only made after test completion, and there is no need to conduct statistical test of significance for trends or shifts.
Eliminating the need to check for statistical significance of drift or shifts makes for a simpler post-processing correction using Method B. This is because all test data points are corrected for. There are different methods of calculation depending upon the number of test tires between control runs. The technical standard describes correction factors for both two and three test tire sequences in ASTM F1650 section 9.3.
ASTM 1650 is an invaluable resource for product and test engineers conducting tire performance evaluations in variable conditions. Finer details not covered in this summary can be found in ASTM F1650. By using the references and tools in this specification, engineers can uncover precise, objective data needed to achieve regulatory compliance and make product development decisions.
